从矩阵角度分析转置卷积
前言
上次从公式角度研究了转置卷积。这次想进一步从矩阵计算角度研究。内容基本上参考这位大神在B站讲解的转置卷积(transposed convolution),他在CSDN也有对应的博文转置卷积(Transposed Convolution)。强烈建议大家去看看B站的视频。我这里的图片都来源于这位大神。
这里只是把我感兴趣的地方做个记录,以便后来查找。我感兴趣的是,从矩阵运算的角度讲,转置卷积为什么能放大图片
转置卷积原文:A guide to convolution arithmetic for deep learning
转置卷积的计算流程
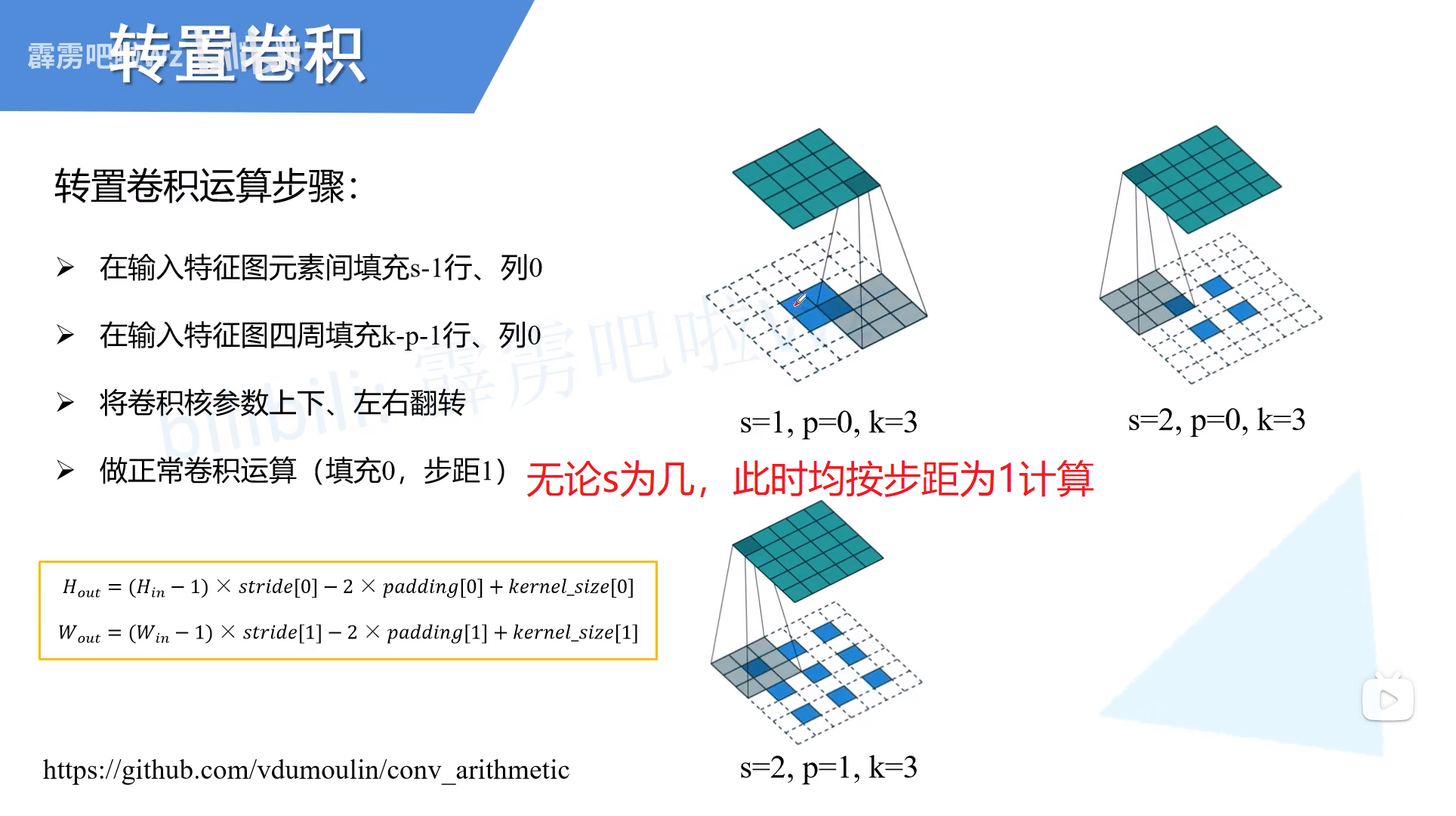
转置卷积和普通卷积的关系
首先明确,转置卷积不是标准卷积的逆运算
普通卷积
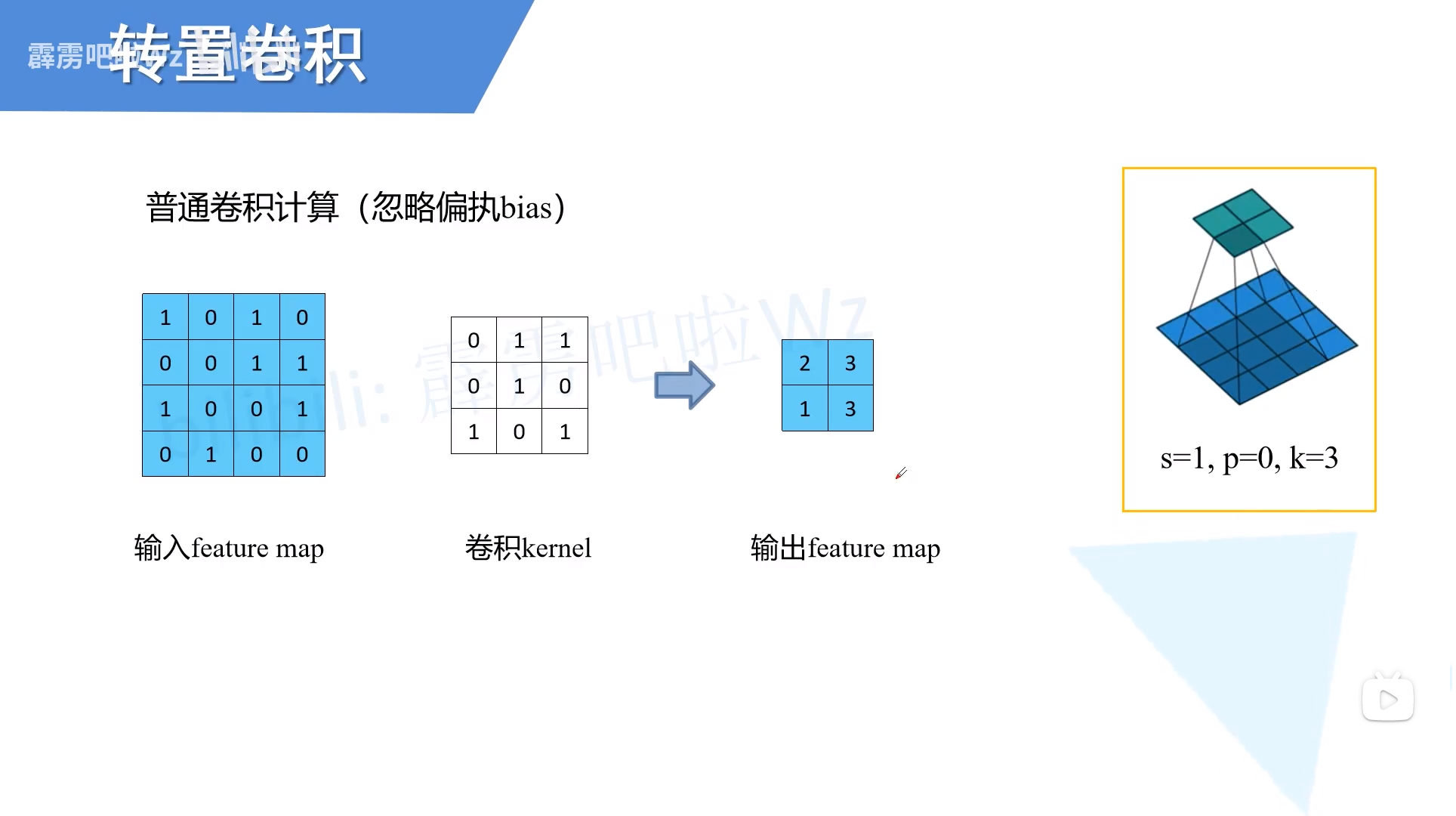
填充卷积核以代替平移
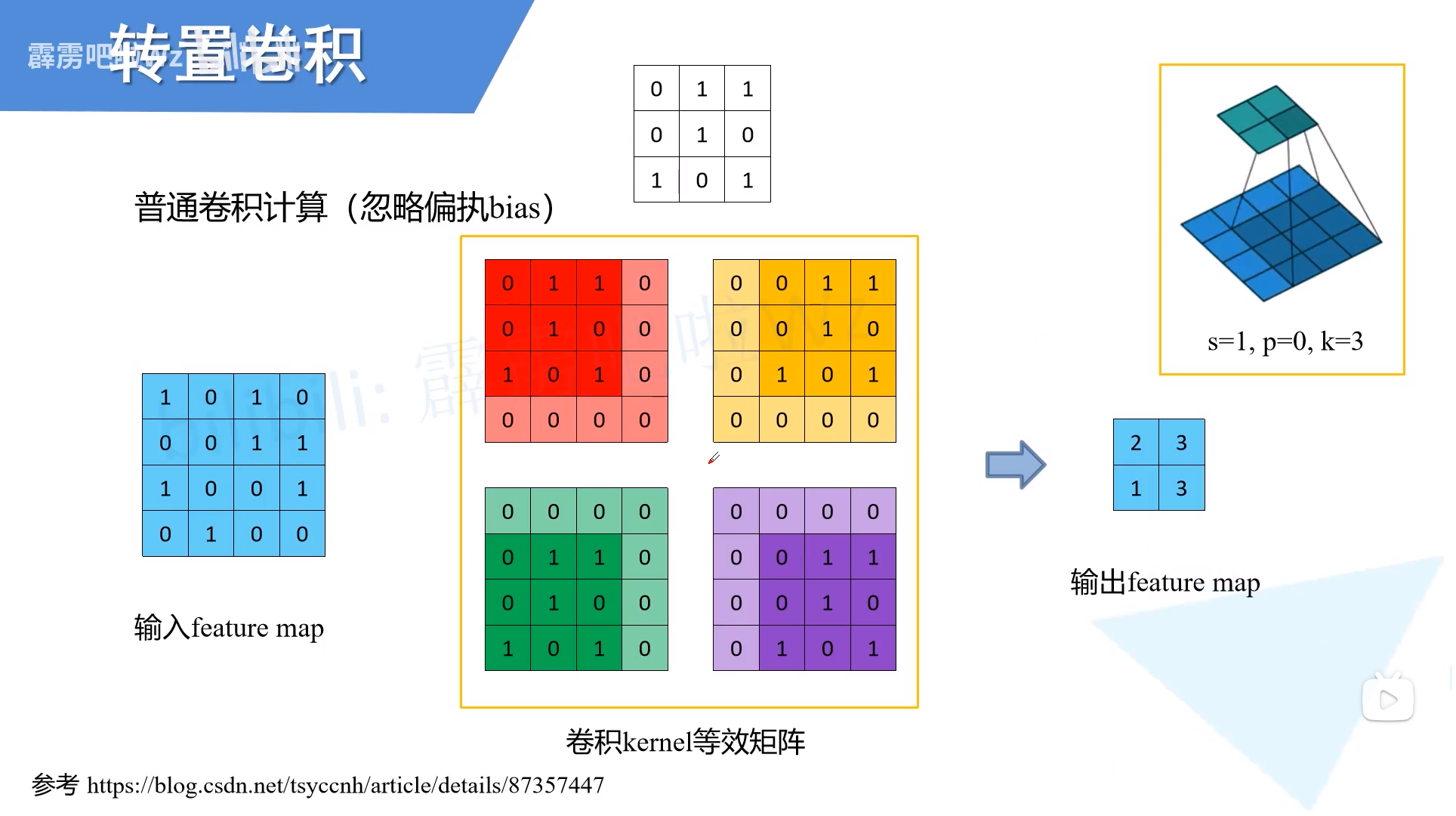
将卷积核和输入展平
展平顺序是先行后列
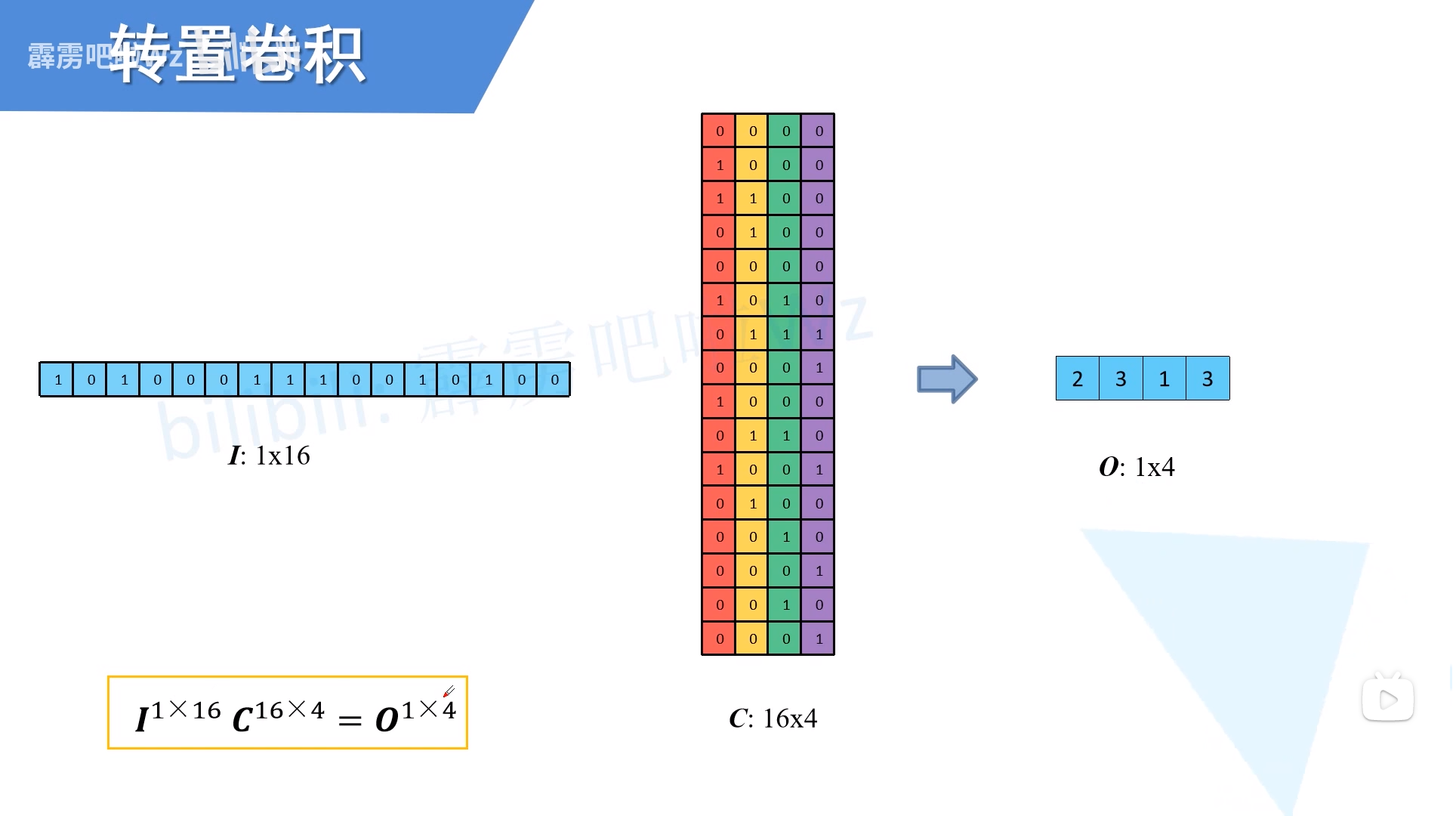
转置卷积
上面那个式子, 。如果已知长度较小的O,想把它变长,怎么办? 等式两边乘上,于是
从维度上看 为1 *16,但因为$C·C^T $不是单位阵,
因此,转置卷积只起到了放大的作用,并不是卷积的逆过程。

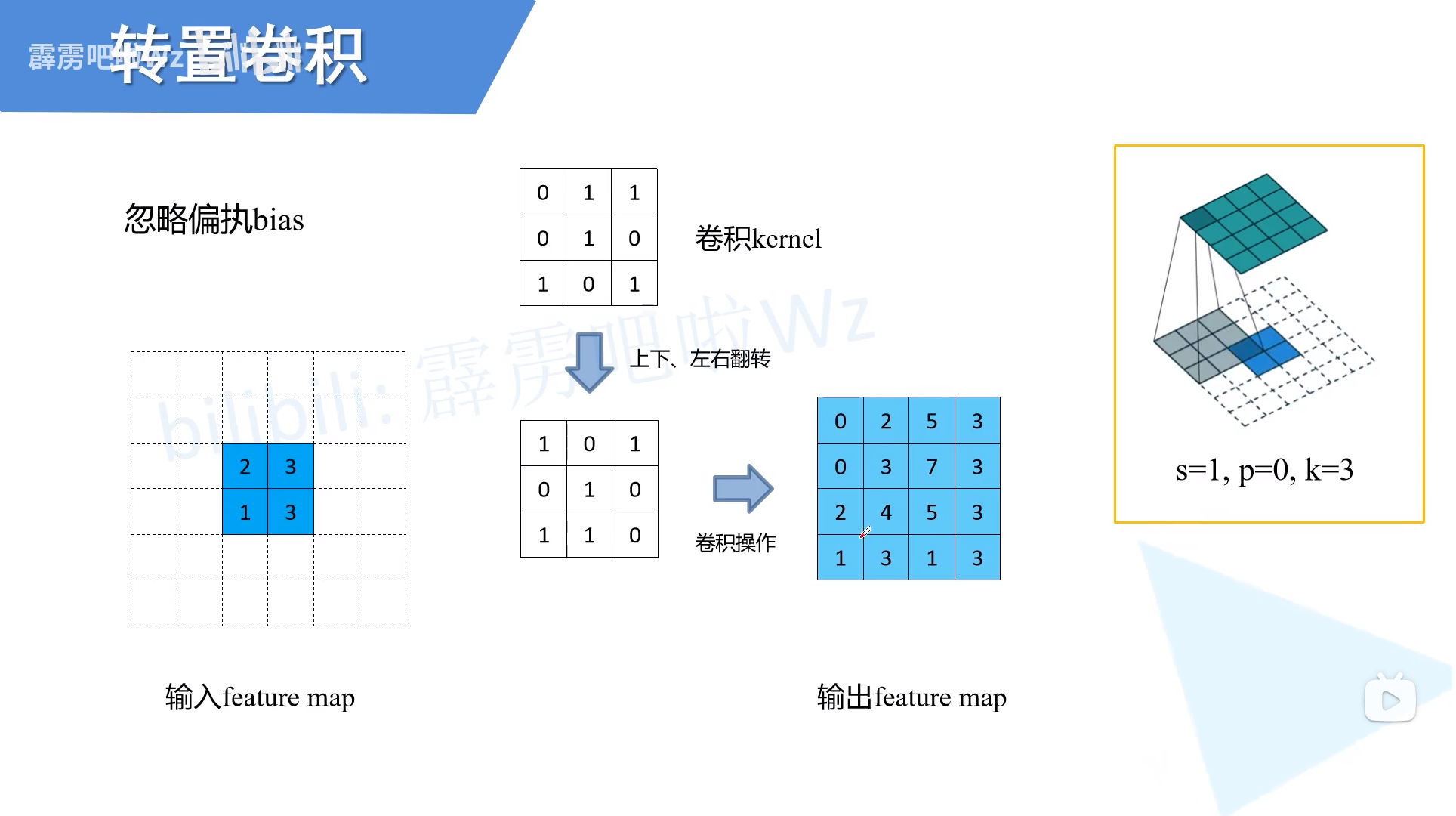
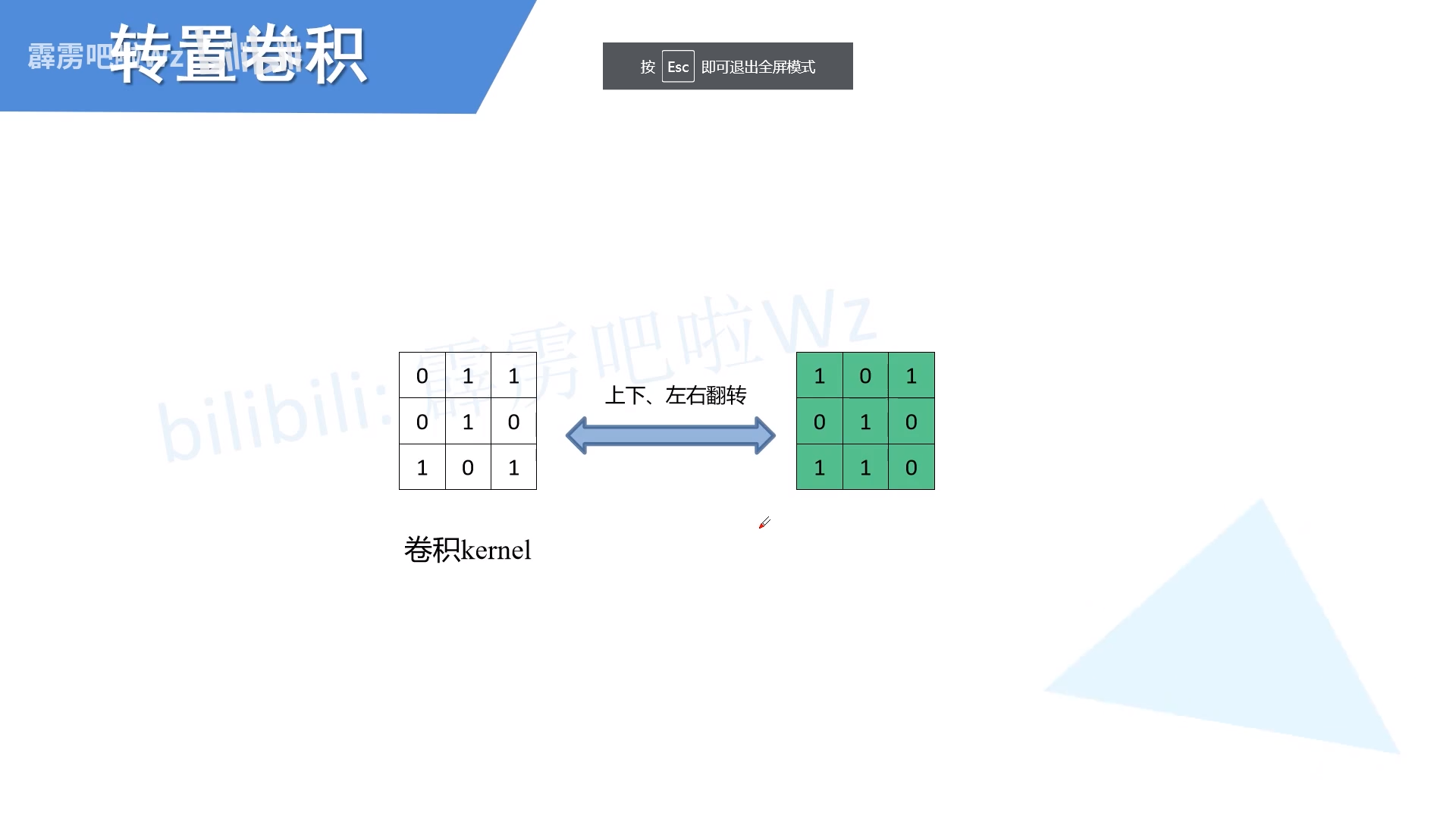
转置卷积核和普通卷积核的关系
我得先说,这里可以不用去看。因为在实际使用的时候,转置卷积核是经过训练得到的,并不会通过上下左右翻转得到与其了解两者的关系,不如直接把转置卷积直接当做一种特殊的卷积。
但是我还是记录一下大佬的讲解。
首先将经过转置的卷积核还原成单个卷积核
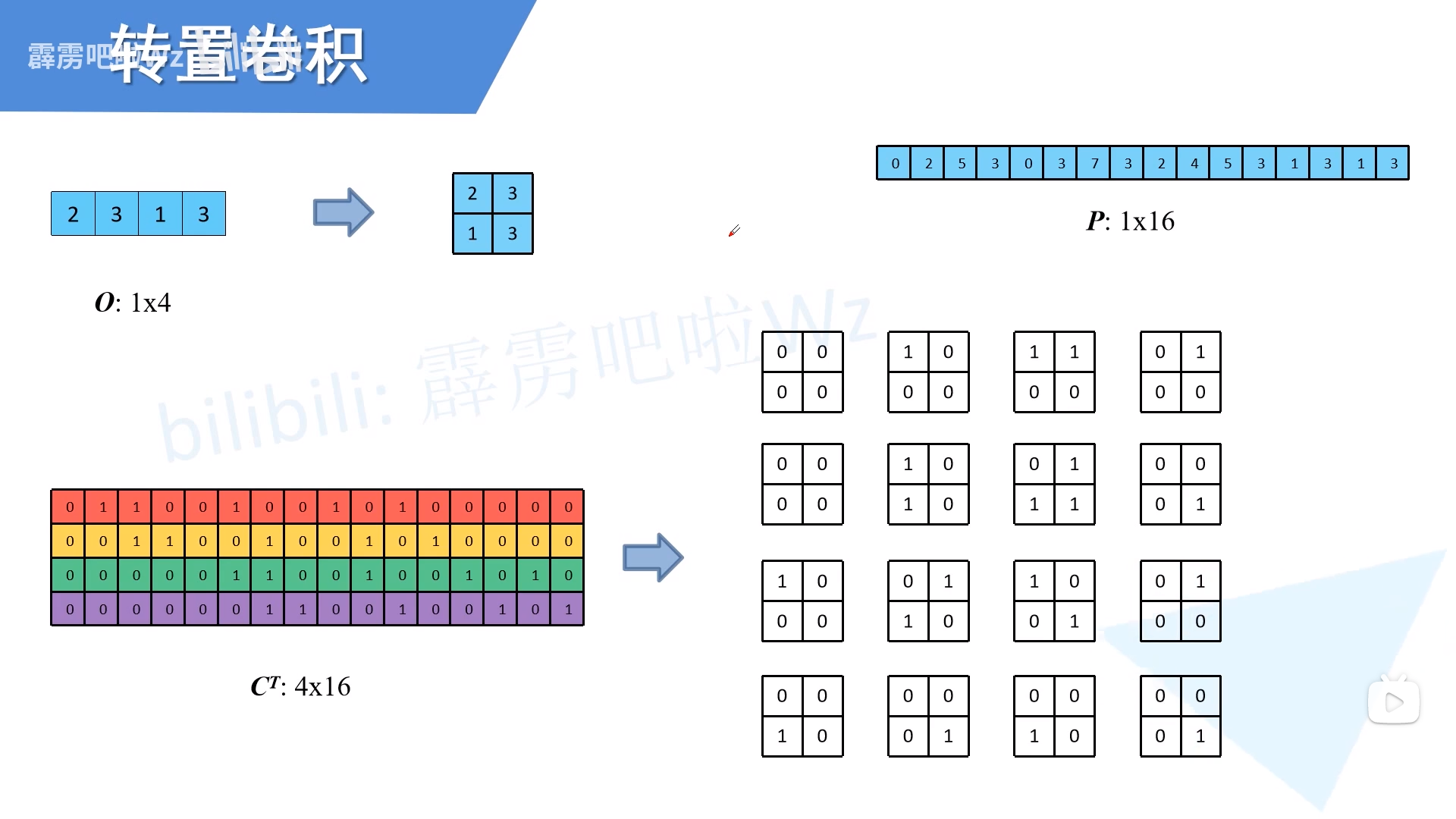
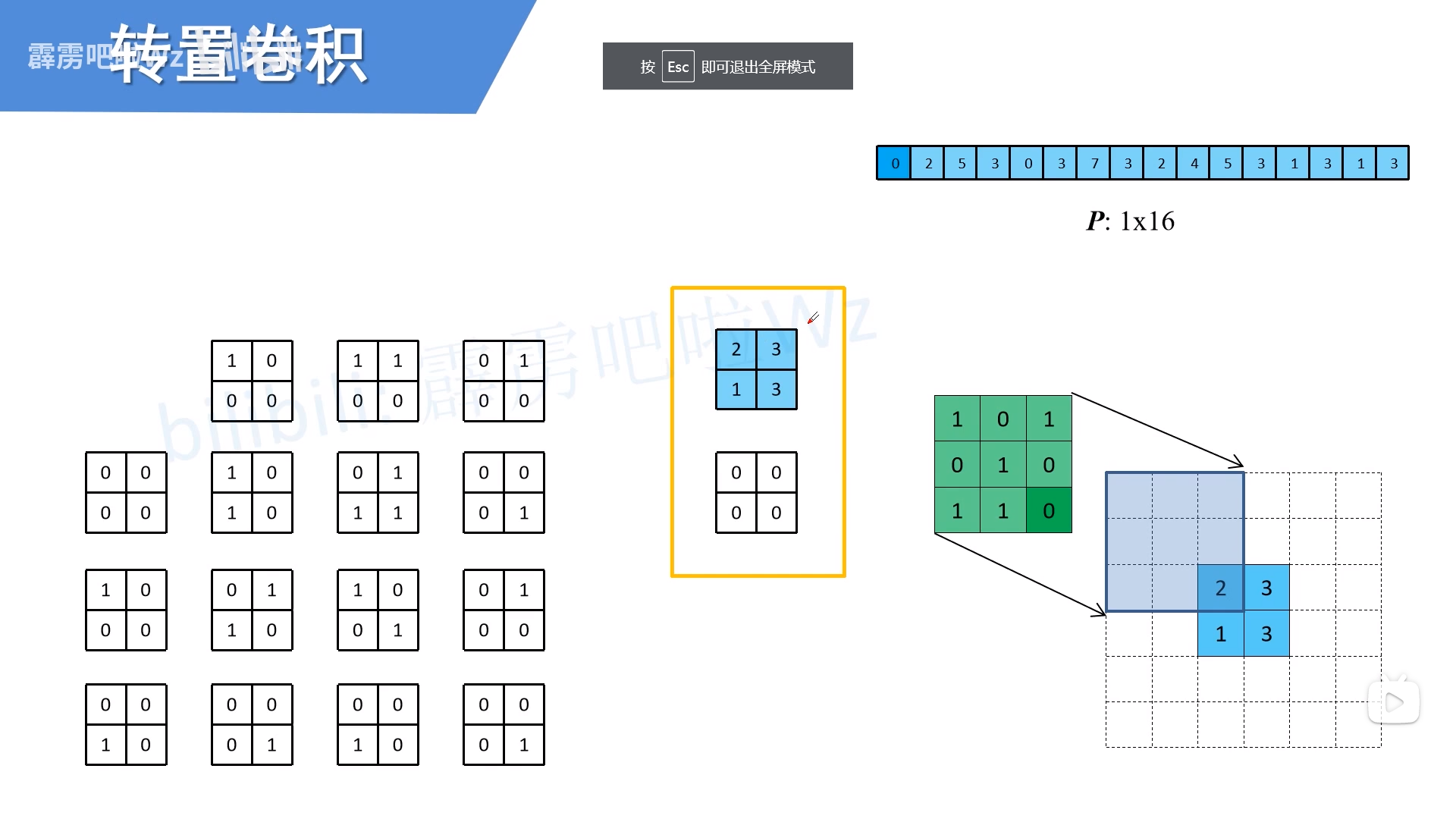
总结
用我研究语义分割同学的话说:转置卷积就是一个会更精细一点的上采样,因为它可训练。
参考
[1] https://www.bilibili.com/video/BV1mh411J7U4?spm_id_from=333.999.0.0